朝会（校長講話）

１１月５日（火）

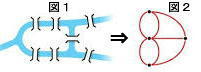
　18世紀の初め、プロシアのケーニヒスベルク（現ロシアのカリーニングラード）を流れるプレーゲル川には、図1のように7つの橋がかかっていました。「同じ橋を2度渡らず、7つの橋をすべて渡って、元の場所にもどれるか」ということが議論になり、スイスの数学者オイラーが、そのような経路は存在しないことを証明しました。この問題を、図2のように数学化すると「一筆書き」ができるかどうか、という問題となります。「一筆書き」ができるための条件は、次の2つです。(1) すべての頂点に集まる辺の数が偶数の場合。(2) 集まる辺の数が奇数の頂点が2つと、それ以外の頂点に集まる辺の数が偶数の場合。（図2のことをグラフ、グラフの点を頂点、頂点を結ぶ線を辺とよぶ）　詳しい説明はしませんが、その2つしかできない理由を考えてみてください。